An Introduction to Causal Mediation Analysis With a Comparison of 2 R Packages
Article information
Abstract
Traditional mediation analysis, which relies on linear regression models, has faced criticism due to its limited suitability for cases involving different types of variables and complex covariates, such as interactions. This can result in unclear definitions of direct and indirect effects. As an alternative, causal mediation analysis using the counterfactual framework has been introduced to provide clearer definitions of direct and indirect effects while allowing for more flexible modeling methods. However, the conceptual understanding of this approach based on the counterfactual framework remains challenging for applied researchers. To address this issue, the present article was written to highlight and illustrate the definitions of causal estimands, including controlled direct effect, natural direct effect, and natural indirect effect, based on the key concept of nested counterfactuals. Furthermore, we recommend using 2 R packages, ‘medflex’ and ‘mediation’, to perform causal mediation analysis and provide public health examples. The article also offers caveats and guidelines for accurate interpretation of the results.
INTRODUCTION
Mediation analysis is a valuable tool in medical and epidemiological studies for identifying causal mechanisms between a treatment or exposure and an outcome [1–3]. Traditionally, mediation analysis is based on normal linear models (e.g., linear regression, linear structural equation modeling), termed traditional mediation analysis [4,5], and has been widely used in empirical studies [2]. However, the traditional approach has faced criticism due to its limitations. Regarding model specifications, it cannot accommodate all types of variables (such as binary outcomes) and a wide range of functional forms [6,7]. Specifically, the estimates obtained by the traditional approach can be biased in the presence of non-linearities or interactions [2]. Furthermore, if researchers include various types of variables or employ flexible techniques reflecting different functional forms, the conventional methods (e.g., the difference or product method for indirect effects) lose their validity [2,3,7,8]. Consequently, the resulting estimates often become uninterpretable. This difficulty in interpreting direct and indirect effects is a critical issue in traditional mediation analysis.
In contrast to the traditional approach, causal mediation analysis (CMA) employs a well-defined distinction between direct and indirect effects through the counterfactual framework. CMA considers the traditional approach as a specific instance, permitting a broader array of outcome variables and sophisticated modeling techniques [9]. As a result, CMA has been progressively employed in medical and epidemiological research to enhance the comprehension of causal mechanisms. However, applying CMA necessitates a solid understanding of theoretical concepts associated with the counterfactual framework, which may be unfamiliar to empirical researchers.
The aim of this study was to provide empirical researchers with a comprehensive understanding of CMA. First, we clarify basic concepts such as nested counterfactuals and the definitions of causal estimands, including the controlled direct effect, natural direct effect, and indirect effect. Second, we illustrate the identification conditions for these causal estimands in an intuitive manner. Third, we outline the practical application of CMA using 2 R packages (R Foundation for Statistical Computing, Vienna, Austria), ‘medflex’ [10] and ‘mediation’ [11]. Specifically, this article focuses on the caveats and guidelines for accurate interpretation by comparing the 2 packages through a public-health-related example.
BASIC FRAMEWORK OF CAUSAL MEDIATION ANALYSIS
In this section, we outline the basic framework pertaining to CMA.
Nested Counterfactuals
The first step in CMA involves clearly defining the causal estimands of interest, such as direct and indirect effects. These estimands are based on nested counterfactuals, which have been extensively discussed in the literature [8,12–14]. For readers unfamiliar with this concept, we first present a brief introduction to causal effects based on counterfactual or potential outcomes [15–18]. For instance, let us consider the preventive effect of influenza vaccination. How can we define the causal effect of the vaccine on an individual? The answer is based on human logical reasoning. Suppose we can observe 2 outcomes (1, infected; 0, not infected) depending on the vaccination status of the individual. One outcome is observed in the vaccinated scenario and the other in the unvaccinated scenario. If the difference between these 2 outcomes is not equal to 0, we can conclude that a vaccination effect is present. This difference, known as the individual causal effect [19,20], is represented as follows:
in which Y1 and Y0 denote potential or counterfactual outcomes under treatment and control conditions, respectively. However, readers may notice that the quantity above is not observable in a concrete sense, as we can only observe either of the 2 outcomes [20,21]. This is the essence of potential or counterfactual outcomes. To circumvent this issue, the standard approach involves focusing on the causal effect on average [18], which is referred to as the average causal effect (ACE) [18,21] or average treatment effect (ATE) [17,22,23]. The ACE represents the average effect of the treatment in comparison to the control across all units [22] and can be expressed as:
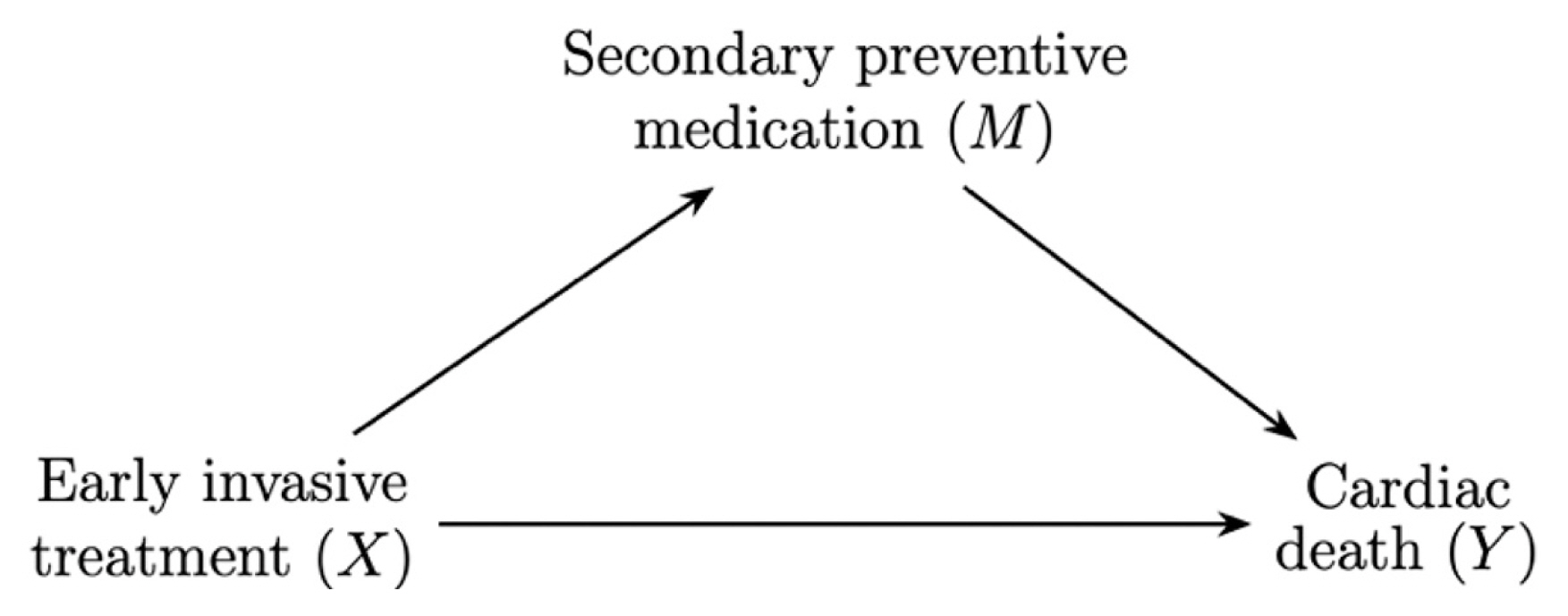
Next, we proceed to nested counterfactuals. Consider the simple example shown in Figure 1 [14]. In the original paper, confounders are included, but we set them aside momentarily to simplify the illustration. The graph represents a hypothetical causal structure in which the application of early invasive treatment, X (1, treatment; 0, control), to patients hospitalized for acute coronary syndrome influences both secondary preventive medication, M (1, provided; 0, not provided), and death, Y (1, deceased; 0, alive). Subsequently, secondary preventive medication affects cardiac death. Here, M is referred to as the mediator.
In CMA, the counterfactual expression of Y is somewhat complex, as it relies on the fact that M is affected by X. Hence, the mediator is also represented as a counterfactual depending on the treatment status. This explains why the term “nested” is used. We will further explain nested counterfactuals using the example provided earlier. Suppose a man is hospitalized for acute coronary syndrome, and that X is equal to 1 if he is assigned to the treatment group. M1 and M0 denote M under the treatment condition and under the control, respectively. The counterfactual expression of the outcome depends on combinations of X (1, treatment; 0, control) and M (M1, M0). For example, Y1M1 denotes the counterfactual cardiac death outcome if the man belonged to the treatment group, and the mediator was at the mediator status that would have been obtained under the treatment condition. Similarly, Y1M0 denotes the counterfactual cardiac death outcome if the man belonged to the treatment group, while the mediator was at the mediator status that would have been obtained under control conditions. Y1M0may seem illogical to some readers because the treatment status (1) differs from the treatment status in the mediator (0). Importantly, however, we are describing the outcome in the counterfactual framework, not the actual occurrence. Here, it is worth mentioning that the mediator in the counterfactual outcomes (Y1M1, Y1M0) can vary among individuals, rather than being fixed at a specific value. Readers will see that the remaining counterfactual outcomes, Y0M1 and Y0M0, are defined similarly.
Although we have thus far limited our focus to binary treatments, this framework can be extended to multicategorical or continuous treatments. For continuous X, we choose 2 certain values, x and x′, of X. Then, the nested counterfactual outcomes were represented as YxMx, YxMx′, Yx′Mx and Yx′Mx′.
Natural Direct and Indirect Effects
In this subsection, we illustrate the direct and indirect effects based on nested counterfactuals. In simple terms, the direct effect refers to the effect of X that is not mediated through M [24]. Readers can easily understand that in Figure 1, the arrow from X to Y represents the direct effect. Furthermore, the figure intuitively suggests why M affected by X should be fixed in some way to formally define the direct effect. Otherwise, an effect may exist through the mediator M. Depending on how the mediator is fixed, 2 types of direct effects have been widely studied in CMA. One is known as the controlled direct effect (CDE), which expresses the average change in the outcome when the mediator is fixed at the value of m for the whole population, but the treatment is changed from x′ to x [12,24]. Using the nested counterfactual notation, the CDE is represented as:
The natural direct effect (NDE) is defined as the change in the outcome if the treatment were set at x versus x′, while the mediator for each individual is set at the value it would have taken for that individual under the treatment status x′ [12,4]. Using nested counterfactual notation, the formal definition of NDE is defined as:
To clarify the difference between the 2 direct effects, we revisit the example in Figure 1. In the example, the CDE(m) represents the average change in cardiac death probability by the treatment while all the mediators were fixed at m. For instance, researchers may examine CDE (1) to understand the treatment effect under the policy of mandating secondary preventive medication for patients. In contrast, the NDE allows secondary preventive medication to vary among patients, which illustrates the concept of “natural” effect.
Next, we will discuss the indirect effect, which represents the impact of the treatment through the mediator of interest [24]. Formally, the natural indirect effect (NIE) describes the average change in the outcome if the treatment were maintained at the status x but the mediator were altered from the value it would take under the treatment status x′, to the value it would take under treatment status x [12]. Using the nested counterfactual notation, the NIE can be expressed as:
A connection exists between NDE, NIE, and ACE. ACE can be broken down into the sum of NDE and NIE (i.e., ACE = NDE + NIE), which aligns with the understanding that ACE represents the total effect of X. However, this is not the sole method for decomposing ACE, as causal effects can be defined on various scales depending on the types of outcomes. For instance, the causal effect for binary outcomes, as demonstrated in Figure 1, is frequently defined on the odds ratio (OR) scales as follows [24,25].
On the OR scale, the product of 2 ORs representing the NDE and NIE is equivalent to the OR for the total effect [24,25].
Identifying Direct and Indirect Natural Effects
NDE and NIE cannot be generally identified based on observed data alone. It is crucial to determine the conditions under which NDE and NIE can be identified. To identify these effects, both consistency and positivity are necessary. Consistency implies that the nested counterfactual Yxm is equal to the observed outcome under X=x and M=m for all x and m, and Mx is equal to the observed mediator when the treatment value is x for all x. The latter states that all treatment values given confounders C have non-zero probabilities between 0 and 1, and all mediator values given confounders and the treatment value also have non-zero probabilities between 0 and 1 [14]. For continuous X and M values, the probability is replaced by the corresponding density value. Additional assumptions are needed to identify NDE and NIE. Various versions of the identification conditions for NDE and NIE exist in the literature. Although these conditions are not mathematically equivalent, they resemble one another. One such version [3,14,24] can be expressed as follows.
Assumption 1 (identification)
NDE and NIE can be identified if:
A1. No unmeasured confounders exist for any pair of treatment and mediator (X, M), treatment and outcome (X, Y), and mediator and outcome (M, Y) given C.
A2. No confounders of the mediator (M)-outcome (Y) relationship are affected by the treatment (X), given C.
Instead of A2, Pearl [12] employed the so-called cross-world independence assumption for identifying NDE and NIE, which states that given C, the counterfactual outcome under the treatment status x and mediator status m is independent of the counterfactual mediator under the treatment state x′ for any m and x≠x′ (i.e., Yxm ⊥ Mx′ | C ∀ m, x≠x′). Importantly, the randomization of X alone does not satisfy the identification conditions in general. This is because confounders of M and Y may exist even if X is randomized [24]. Therefore, like other causal inferences from observational studies, researchers need to carefully include confounders based on the causal structures. Detailed descriptions and technical proofs of the identification and related assumption, as well as presenting the pioneering frameworks of the NDE and NIE are provided in [12,26,27]. Moreover, Pearl [28,29] suggested the implications of the cross-world independence assumption and related alternatives under mild conditions in terms of the non-parametric structural equation models. A different and stringent version of the cross-world independence assumption has been articulated by Imai et al. [6,30,31].
Once a proper set of confounders is adjusted, conditional CDE, NDE, and NIE are defined as shown below.
For binary outcomes, the corresponding 3 effects using ORs are defined as follows.
To explain how the conditional expectations of the nested counterfactuals are calculated, we focus on the conditional expectation of YxMx′ given the confounders C. This is the most enigmatic aspect of the situation, because YxMx′is never observed in the real world. The conditional expectation is derived from Pearl [12]’s mediation formula (with M assumed to be discrete), written as:
and the last 2 expressions are provided in [13]. In this formula, ℙ[m|x′, C] denotes the probability of M given X=x′, C. Because the second expression is not directly applicable to real-world data owing to the counterfactuals, we use the third expression in practice. That expression is derived through consistency in conjunction with the described identification assumptions.
Most R packages implementing CMA are based on the mediation formula, although their versions differ. The R package ‘mediation’ estimates the marginal or population-averaged NDE and NIE by averaging the conditional NDE and NIE over the confounders [11]. Because its key causal estimand is  , it requires fitting 2 separate models for the mediator and the outcome. In contrast, the other R package ‘medflex’ employs the fourth and last expressions. The weighting method in this package uses ℙ[m|x′, C]/ℙ[m|x, C] as weights in the fourth expression (function neWeight), and the imputation method uses
, it requires fitting 2 separate models for the mediator and the outcome. In contrast, the other R package ‘medflex’ employs the fourth and last expressions. The weighting method in this package uses ℙ[m|x′, C]/ℙ[m|x, C] as weights in the fourth expression (function neWeight), and the imputation method uses  as the imputed outcome in the fifth expression when x is not equal to the observed status for each individual (function neImpute). Detailed examples using both R packages are provided in the next section.
as the imputed outcome in the fifth expression when x is not equal to the observed status for each individual (function neImpute). Detailed examples using both R packages are provided in the next section.
APPLICATION OF CAUSAL MEDIATION ANALYSIS VIA R PACKAGES
In this section, we present a detailed illustration of 2 R packages, ‘medflex’ and ‘mediation,’ for CMA. Both packages not only support various types of treatments, mediators, and outcomes, but also allow flexible regression modeling. For this reason, they have been broadly used in many areas. However, notwithstanding their widespread use, there are some caveats that users should note. The detailed results of the following tables and corresponding R code are presented in the Supplemental Material 1.
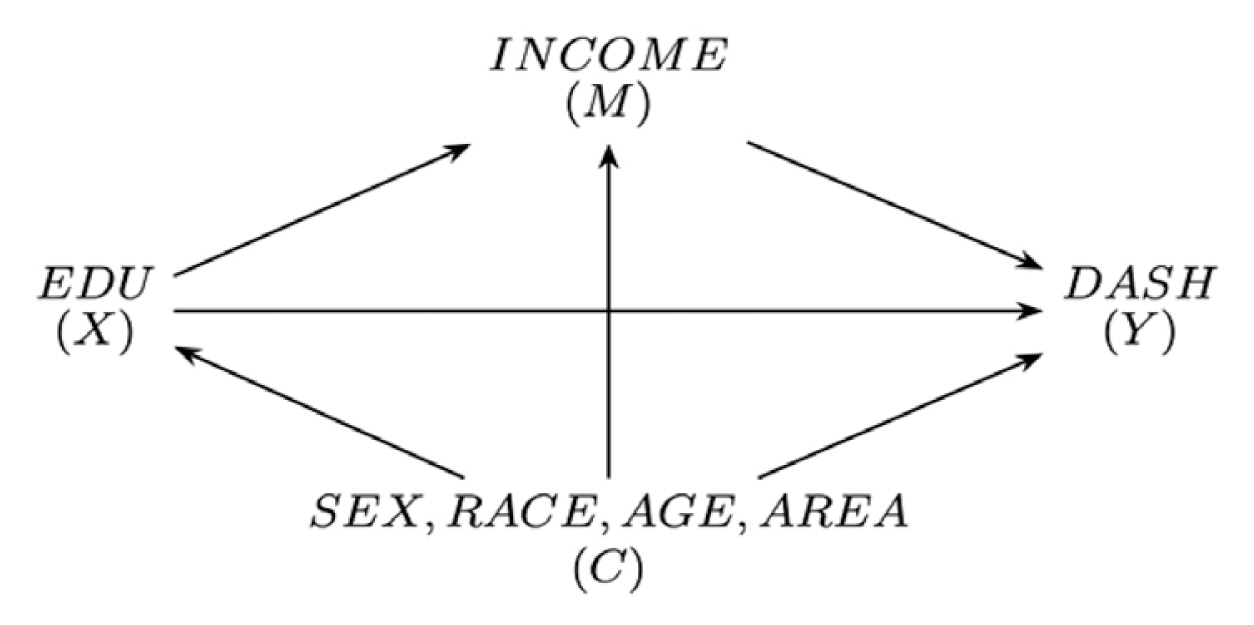
For comparison, we generated hypothetical data based on Patel et al. [32], who investigated the causal relationship between education and the Dietary Approach to Stop Hypertension (DASH) diet, which prevents risk factors for cardiovascular diseases [32]. In the data, education (EDU) is a multicategorical treatment (0, degree or equivalent; 1, higher education below degree level; 2, general certificate of secondary education; 3, no qualification), annual income (INCOME) is a binary mediator (1, higher than 15 850 £/y; 0, lower than 15 850 £/y), and the outcome DASH score (DASH) represents the degree of compliance to the dietary approach to stop hypertension (range, 8 to 40). To provide the examples for both binary and continuous outcomes, we dichotomized the DASH score into the binary variable DASH_B. DASH_B indicates whether an individual possesses a higher-than-average DASH score (1, high; 0, low). In addition, 4 confounders (SEX, RACE, AGE, and AREA) are included in the model. The hypothesized causal structure is depicted in Figure 2.
First, we deal with the binary outcome DASH_B using the 2 R packages. The weighting-based method [13] of ‘medflex’ computes the ratio of the conditional probabilities of the mediator given the treatment state x′ and covariates to that given the treatment state x and covariates, with neWeight function. Therefore, it is necessary to fit a model for the mediator. We used logistic regression for the binary mediator INCOME (M) as below. In the regression model, Dj (j=1, 2, 3) refers to a dummy variable that equals 1 only when X=j, and 0 otherwise (reference group, X=0). In addition, AREA is also transformed into the 5 dummy variables (reference, AREA=1), and the squared term of AGE (AGE2) is included.
On the contrary, the imputation-based method does not require the specification of the mediator model [10]. Instead, the method requires an imputation model to impute the nested counterfactual using fitted values of conditional expectation given the mediator, confounders, and the opposite status of the observed treatment via the neImpute function. In this example, we consider the following imputation model:
With the expanded data from either the weighting or the imputation method, the package computes the estimates of (conditional) NDE and NIE. However, readers who utilized ‘medflex’ for the first time may be confused in finding the estimates of conditional NDE and NIE because the interpretation is obtained via the natural effect model [8,13]. This is a regression model used for the nested counterfactual so that regression coefficients can be directly interpreted as conditional NDE or NIE. In this example, the natural effect model (or logistic natural effect model) is represented as follows:
where dj indicates the value of 1 only when x=j (j=1, 2, 3) and 0 otherwise, and
For each method, the estimates in each row of EDU01~03 correspond to the estimates of the conditional NDE (γ̄01 ~ γ̄03), while the estimates in each row of EDU11~13 refer to the estimates of the conditional NIE (γ̄11 ~ γ̄13). In the table, the estimates from the weighting-based method show slight differences compared to those obtained with the imputation-based method; however, the signs and hypothesis testing exhibit similar trends. Notably, these estimates were calculated on the logit scale, using a logistic natural effect model. As a result, it is useful to exponentiate the estimates as follows (we simply used the results for groups 0 and 1 from the weighting-based method), which leads to the estimates of conditional NDE and NIE on the OR scale:
We conclude that if an individual had a higher education level below a degree (group 1) compared to a degree or equivalent (group 0), it directly reduces the odds (the ratio of the probability of having higher DASH status to the probability of having lower DASH status) by approximately 0.735 times, given individual characteristics (SEX, RACE, AGE, and AREA). Similarly,
The third column in each method refers to the measures of proportion mediated [24], which are defined as the ratio of NIE to the total effect. In fact, these measures were not originally supported in the ‘medflex’ package, but we provide R code for readers in the online Supplemental Mateial 1. In practical studies, these measures may offer valuable information about the extent of mediation. However, users should be careful when utilizing them, as they can be larger than 1 when NDE and NIE have different signs. In this example, both estimates have the same sign. Additionally, these measures should not be interpreted on the OR scale, as they are calculated on the logit scale.
Next, we will examine the results from the ‘mediation’ package. Table 2 displays the results derived from the same dataset. Unlike ‘medflex,’ this package executed separate models for each pair (0 and 1, 0 and 2, and 0 and 3). We combined the 3 tables into 1 for easier comparison. In this package, ACME indicates the average causal mediation effect and ADE the average direct effect [6,11]. ACME and ADE correspond to NIE and NDE, respectively. The estimates generated using the same data with the ‘mediation’ package can be found in Table 2.
Readers may find it challenging to compare the estimates in Table 2 with those in Table 1. We can attribute this discrepancy to 2 primary factors. First, the estimates provided by the ‘mediation’ package for binary outcomes are calculated on the risk difference scale [11,25]. As a result, it is essential to recognize that all estimates from this package should be interpreted as an increase in probability, not as a ratio [11]. Second, as briefly mentioned earlier, ADE and ACME in the ‘mediation’ package correspond to the marginal NDE and NIE, respectively. In contrast, the ‘medflex’ package provides the conditional NDE and NIE by default (To compute the marginal estimates in ‘medflex’, users can employ the ‘xFit’ option along with additional model fitting; the corresponding R code is available in the Supplemental Material 1). For instance, ADE and ACME estimates of EDU =1 in Table 2 indicate the following quantities. Consequently, the estimates on the OR scale and those on the difference scale have different interpretations in practice. Importantly, estimates on the OR scale and those on the difference scale have different practical interpretations.
Now, let us examine a case with a continuous outcome. The hypothesized model in the subsequent results was identical to the previous binary outcome model, except that the continuous DASH score was utilized. The estimates from both packages are displayed in Tables 3 and 4. The following results were also derived using the natural effect models. The model specification is akin to the binary model, but the identity link was employed instead of the logit link.
In contrast to the binary outcome case, we observe that the results produced by the 2 different packages are similar. This similarity arises because the causal estimands for both packages are defined on the same scale for continuous outcomes (i.e., difference). However, it is important to emphasize that the estimates obtained through ‘medflex’ and ‘mediation’ represent the conditional and marginal natural effects, respectively. Additionally, it is worth noting that the difference between conditional and marginal estimates can be substantial when interactions are present (e.g., an interaction between EDU and RACE). In the current example, we have:
CONCLUSION
This article presents the counterfactual framework of CMA. Specifically, it elaborates on the definitions of CDE, NDE, and NIE using nested counterfactuals and provides examples. Unlike traditional mediation analysis based on linear models, CMA incorporates various types of variables and offers flexible modeling. Furthermore, the CMA framework provides simple and clear interpretations for NDE and NIE estimates, regardless of the model’s complexity. These features are prominent advantages of CMA over traditional mediation analysis. Concerning identification conditions, directed acyclic graphs show promise as a tool for researchers in confounder selection. Ultimately, the true value of CMA lies in its ability to prompt researchers to clarify the causal estimands they wish to examine in mediation analysis. This concept is well illustrated in the detailed comparisons of the 2 R packages, ‘medflex’ and ‘mediation,’ which can produce different estimates from the same data. In particular, practical analysis using these packages should be conducted with a careful and comprehensive understanding of the quantities they aim to provide. In addition to the 2 R packages, SAS and SPSS macros are available for mediation analysis. For readers interested in exploring the major technical differences among various CMA methods, we recommend referring to Starkopf et al. [33].
Indeed, the identification and interpretation of causal estimands have been recognized as the primary focus in CMA. While not discussed in detail in this paper, important topics include the multiple mediator approach in the presence of confounders affected by treatments (i.e., intermediate confounding), evaluating bounds under relaxed conditions [34,35], and targeting different definitions of NDE and NIE [9,36,37]. The advancement of CMA methodology in recent years allows us to unravel the meaning of causal estimands and the underlying mechanisms in more complex research problems. In this regard, the appropriate application of CMA in research will not only aid in understanding causal mechanisms from a theoretical perspective but also contribute to establishing data-driven evidence for health policy in practice.
SUPPLEMENTAL MATERIALS
Supplemental material is available at https://doi.org/10.3961/jpmph.23.189.
Notes
CONFLICT OF INTEREST
The authors have no conflicts of interest associated with the material presented in this paper.
AUTHOR CONTRIBUTIONS
Both authors contributed equally to conceiving the study, analyzing the data, and writing this paper.
FUNDING
None.
ACKNOWLEDGEMENTS
None.